Bismillahirrohmanirrohim

Dengan menyebut nama Allah yang maha pengasih dan penyayang

Suherman

Saatnya berbagi pengetahuan

Suherman

Selamat datang pengunjung budiman

Nurul fikri

Nurul fikri mendidik diri, mendidik generasi baru

Nurul fikri

Kita maju bersama Allah menuju masa depan cemerlang

Selasa, 30 Oktober 2012

SIMAK UI 2011 Mat IPA kode 511

21.31    1 comment

Read More

UTS Kalkulus1 okt 2012 BIO-FIS

18.45    No comments
 
Mau lihat pembahasannya silahkan klik pembahasan

Read More

UTS KALKULUS 1 okt 2012

18.23    No comments
                               Mau lihat pembasannya klik pembahasan UTS kalkulus
Read More

Senin, 29 Oktober 2012

Pertidaksamaan

23.08    No comments

Read More

Minggu, 21 Oktober 2012

Lingkaran

21.47    No comments

  
(A)  ( -4, -2)
(B)  ( -4, 2)
(C) ( -4, -4)
(D) ( -4, 4)
(E) ( -4, 8)             SNMPTN 2012 Kode 484

Pembahasan :
Jelas x titik singgungnya x = - 4, untuk mencari y nya subtitusikan x ke persamaan lingkarannya.

                          
diperoleh y = 2. jadi titiknya adalah ( -4, 2)
Read More

Soal SNMPTN dan SIMAK UI teori Peluang

19.46    No comments
Didalam kotak terdapat 3 bola biru, 6 bola merah dan 2 bola putih. Jika diambil 7 bola tanpa pengembalian, maka peluang banyak bola merah yang terambil tiga kali, banyak bola putih yang terambil satu kali dan sisanya bola biru adalah ...
A. 1/330
B. 2/33
C. 4/33
D. 16/55
E. 1/12                  SNMPTN 2012 kode : 533


Jwb : bola merah yang terambil tiga kali banyak bola putih yang mungkin adalah: 3m,1p,3b

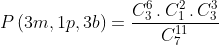
Jadi  P(3m, 1p, 2b) = 4/33
mau lihat soal - soal peluang lainnya silahkan klik bismillah
Read More

Senin, 15 Oktober 2012

Cara menulis rumus matemtika

21.08    No comments
Untuk menulis rumus matematika dalam office dengan menggunakan equetion sedangkan dalam postingan blog dengan bahasa latex
Read More

Minggu, 14 Oktober 2012

Limit Aljabar

21.29    No comments
SPMB 2003 regional III
\displaystyle \lim_{x \to \infty} \left( 3x - 2 - \sqrt{9x^2 - 2x + 5} \right) = ...
(A)   -\frac{5}{6}
(B)   -2\frac{1}{3}
(C)   -1\frac{2}{3}
(D)   2\frac{1}{3}
(E)   \frac{5}{6}

Jawab :
\begin{aligned} \displaystyle \lim_{x \to \infty} \left( 3x - 2 - \sqrt{9x^2 - 2x + 5} \right) &= \lim_{x \to \infty} \left( 3x - \sqrt{9x^2 - 2x + 5} \right) - 2 \\ &= \lim_{x \to \infty} \left( \sqrt{(3x)^2} - \sqrt{9x^2 - 2x + 5} \right) - 2 \\ &= \frac{0 - (-2)}{2\sqrt{9}} - 2 \\ &= -1\frac{2}{3} \end{aligned}
\therefore   Jawab : C
catatan :
\displaystyle \boxed{ \lim_{x \to \infty} \left( \sqrt{ax^2+bx+c}-\sqrt{ax^2+px+q} \right) = \frac{b-p}{2\sqrt{a}}}
Read More
Langganan: Postingan (Atom)